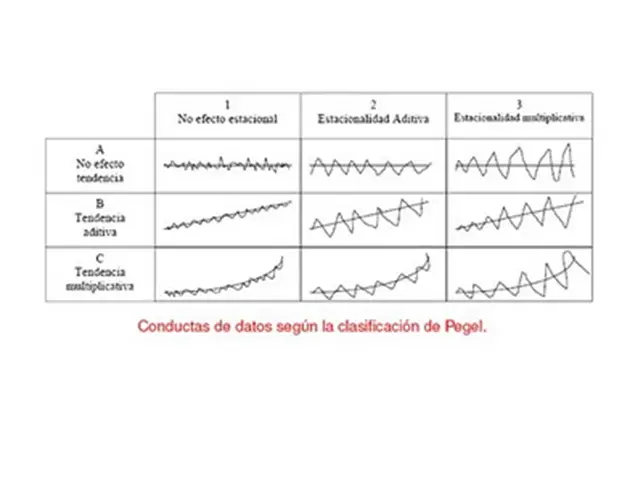
En el mundo del análisis de datos, es común encontrarse con datos que varían a lo largo del tiempo. Estas variaciones temporales tienen un patrón recurrente y, para comprenderlos adecuadamente, es necesario realizar un análisis de series temporales. Este tipo de análisis nos permite descomponer los datos en componentes que representan tendencias, estacionalidad, ciclos y ruido. En este artículo, exploraremos en detalle cómo realizar un análisis de series temporales y cómo identificar las variaciones estacionales que existen en los datos. ¡Acompáñanos en este fascinante viaje por el mundo de la visualización y la interpretación de datos cronológicos!
Análisis de series de tiempo: definición
Al preparar un presupuesto de caja (o las previsiones en las que se basa), es posible llegar a estimaciones válidas utilizando métodos estadísticos. El análisis de series de tiempo se ocupa de las formas numéricas en las que se puede utilizar el pasado para predecir el futuro.
El término análisis de tendencias también se utiliza para describir la técnica examinada en este artículo. Es una herramienta útil para pronosticar ventas futuras, pero también puede usarse en otras circunstancias.
En resumen, la idea del análisis de series de tiempo se basa en el supuesto de que los datos seguirán moviéndose en la misma dirección en el futuro que en el pasado.
Ejemplo
Apoyemos la definición anterior con un ejemplo.
Supongamos que un fabricante de calzado vende diferentes cantidades de pares de zapatos durante varios meses. Estos datos se presentan de la siguiente manera:
Mes 1 10 000 Mes 2 11 000 Mes 3 12 000 Mes 4 13 000 Mes 5 14 000 Mes 6 15 000 Mes 7 16 000
Obviamente, si la tendencia que se muestra en la tabla anterior continúa al ritmo anterior, las ventas de zapatos de la empresa podrían estimarse en 17.000 pares en el octavo mes y 18.000 pares en el noveno mes.
Por supuesto, este es un ejemplo muy sencillo; La vida, por otra parte, rara vez es tan sencilla. También vale la pena considerar durante cuánto tiempo es probable que se mantenga este aumento.
Antes de continuar, exploremos técnicas útiles para predecir datos simples. Estas técnicas básicas son esenciales para comprender todo el concepto.
Si cada cambio mensual es constante
En el ejemplo anterior, podemos pronosticar las ventas futuras observando que las ventas de zapatos han aumentado en 1000 cada mes. Si utilizamos la última cifra conocida de 16.000 pares de zapatos en el mes 7, podemos simplemente agregar 1.000 para llegar a un pronóstico de 17.000 pares en el mes 8, y así sucesivamente.
Calcular el cambio en las ventas mensuales promedio
Se puede utilizar una técnica más compleja para llegar a la misma respuesta. Esta técnica es útil cuando cada cambio mensual es diferente.
Si se compara el número de ventas del séptimo mes con el número del primer mes, hay un aumento de 6.000 pares. Al dividir este número por el número de cambios mensuales en nuestros datos, podemos encontrar un cambio promedio por mes.
El número de veces que cambia el mes es 6, que es el número de “espacios” entre meses (o el número total de meses menos 1). Presentado como una ecuación, esto resulta en:
Cambio promedio de ventas mensuales = (Ventas del último mes – Ventas del primer mes) / (Número de meses – 1)
= (16.000 – 10.000) / (7 – 1)
= 1.000 (corresponde a las expectativas)
A su vez, el número 1.000 se puede sumar a los datos de ventas del séptimo mes (es decir, 16.000) para obtener una previsión de 17.000 pares de zapatos vendidos en el octavo mes.
Análisis de series temporales: gráficos
El mismo resultado se puede generar gráficamente. Tomando la misma zapatería como ejemplo, podemos expandir el gráfico según los datos reales para formar una línea de pronóstico.
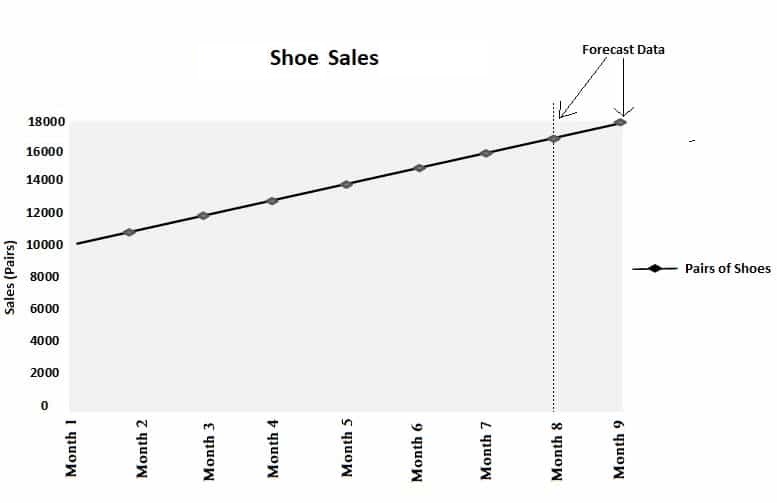
Si los valores reales no cambian a un ritmo constante, el uso de un gráfico seguirá dando el mismo resultado, suponiendo que la línea pasa por el primer y el último punto.
Análisis de series de tiempo: fórmula
Los datos del ejemplo se pueden expresar mediante la siguiente fórmula:
y = mx + c
Dónde
- y es la cantidad prevista
- m es 1.000 (el importe del aumento mensual)
- x es el número de meses desde el mes de inicio
- c es 10.000 (el número de ventas en el mes inicial)
Para crear un pronóstico para el mes 8, el cálculo se ve así:
Pronóstico = (1000 x número de meses desde el mes 1) + 10 000
y (el pronóstico) = (1000 x 7) + 10 000
= 17.000 (corresponde a las expectativas)
Esta fórmula funciona porque se basa en una ecuación lineal.
Series temporales y variaciones estacionales.
En la sección anterior simple información histórica Se utilizó para hacer una estimación o pronóstico de tendencias futuras. Se suponía que las influencias cíclicas, las llamadas fluctuaciones estacionales, no influyen en los datos.
Por lo tanto, esta sección examina cómo se pueden utilizar los datos históricos, que pueden verse afectados por fluctuaciones cíclicas regulares, para crear un pronóstico.
Las medias móviles suelen ser útiles para analizar datos históricos basándose en los dos elementos principales siguientes:
- Tendencia: la dirección general en la que se mueven los datos.
- Fluctuaciones estacionales: movimientos predecibles en los datos que ocurren en ciclos regulares.
La técnica de promedios móviles que se muestra aquí se puede utilizar en determinadas circunstancias para generar los siguientes tipos de datos para presupuestos de efectivo:
- Previsiones de unidades de ventas
- Predicciones de precios
- Previsiones de nivel de producción
En todas estas situaciones, la tecnología sólo proporciona datos válidos si los movimientos pasados de los datos proporcionan una buena base para predecir el futuro.
¿Cómo funcionan las medias móviles?
Una media móvil es una serie de promedios calculados a partir de una serie de datos (por ejemplo, ventas mensuales o costes laborales). Los dos puntos siguientes se aplican a una media móvil:
- Cada promedio se basa en la misma cantidad de datos (por ejemplo, al observar tres datos se obtiene un promedio móvil de tres puntos).
- Cada promedio posterior se mueve una pieza con los datos de la serie temporal, lo que significa que se utiliza un nuevo dato y se descarta un dato antiguo en comparación con el promedio anterior.
Ejemplo
Supongamos que, por razones tecnológicas, la fábrica de una empresa manufacturera utiliza un proceso de fabricación que se ejecuta en un ciclo de tres semanas. Al final de cada período de tres semanas, se limpian los contenedores de producción y se reinicia el proceso.
A medida que los trabajadores de las fábricas se vuelven cada vez más capaces de controlar el proceso, la producción aumenta gradualmente. Las cifras de producción de las últimas semanas son las siguientes:
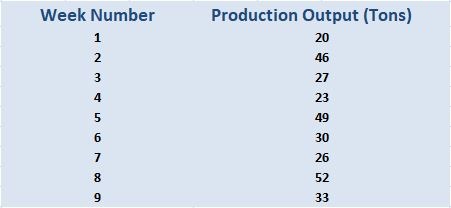
Dado que el ciclo de tres semanas afecta la producción, es posible calcular una media móvil de tres puntos de la siguiente manera:
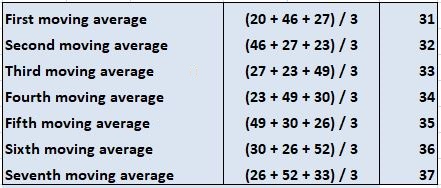
Un punto importante es que avanzamos a lo largo de la lista de datos. En este sencillo ejemplo, que contiene 9 fechas (una por cada semana), no es posible encontrar promedios de tres puntos adicionales. Después de 7 cálculos hemos llegado al final de los números.
Aquí hemos elegido la cantidad de datos que se promediarán a la vez para que corresponda con la cantidad de puntos en un ciclo completo (en este caso, el ciclo de producción de tres semanas de la empresa fabricante).
Al seleccionar tres puntos que corresponden al número de semanas del ciclo de producción, siempre tuvimos un ejemplo de producción de cada tipo de semana en nuestro promedio.
Esto significa que cualquier impacto en el promedio por la inclusión de la primera semana se anula al incluir los datos de la segunda y tercera semana en el ciclo de producción.
Por lo tanto, siempre debemos tener cuidado al calcular las medias móviles de modo que cada media contenga exactamente un ciclo completo.
Encuentra la línea de tendencia
Utilizamos promedios móviles para determinar la línea de tendencia. Esto se puede utilizar para mejorar la previsión de ventas. Una línea de tendencia es una línea que muestra una tendencia que se puede trazar en un gráfico.
Al determinar una línea de tendencia, cada promedio se refiere a los datos que comienzan desde su punto medio, como se muestra en la disposición de los números que acabamos de calcular.
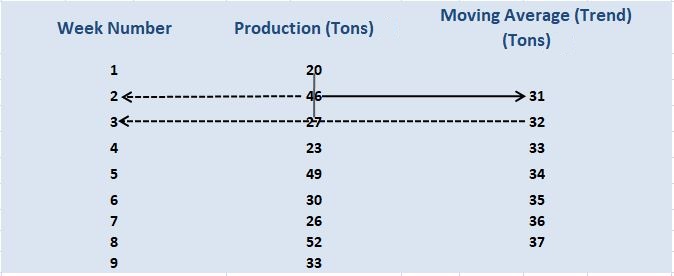
Esto significa que el primer promedio que calculamos (31 toneladas) se puede utilizar como punto de tendencia para la semana 2, mientras que el segundo punto (32 toneladas) forma el punto de tendencia para la semana 3 (ver líneas de puntos). El resultado es doble:
- Sabemos exactamente dónde está la línea de tendencia para cada período.
- Disponemos de una base a partir de la cual se pueden calcular las fluctuaciones estacionales.
Cálculo de fluctuaciones estacionales.
Aunque utilizamos nuestros datos limitados en este ejemplo, podemos ver cómo se calculan las fluctuaciones estacionales. Son la diferencia entre los datos reales en un punto y la tendencia en el mismo punto.
Estas variaciones estacionales se muestran en la columna derecha de la siguiente tabla. Se utilizan como datos las características ya calculadas en la página anterior. Toda la información se da en toneladas.

En este ejemplo, las fluctuaciones estacionales se repiten de la siguiente manera:
- En la primera semana del ciclo de producción, la producción siempre está 10 toneladas por debajo de la tendencia.
- En la segunda semana, la producción supera la tendencia en 15 toneladas
- En la tercera semana, el volumen de producción se sitúa regularmente 5 toneladas por debajo de la tendencia.
Tenga en cuenta la forma en que se utilizan los signos más y menos para indicar variaciones estacionales. Debe tener cuidado de calcularlos con precisión.
- En este caso, un signo más significa que la cifra de producción real está por encima de la tendencia (ver semana 2).
- En este caso, un signo menos significa que la cifra de producción real está por debajo de la tendencia (ver semana 3).
Utilizando los mismos datos, la producción para semanas futuras se puede calcular de la siguiente manera:
- Estima dónde estará la tendencia en la semana seleccionada
- Considere las variaciones estacionales según la semana correspondiente del ciclo.
La producción proyectada para las semanas 10 a 12 será la siguiente:

En este caso, calcular la tendencia prevista es sencillo. Esto se debe a que la producción aumenta continuamente en 1 tonelada cada semana.
Uso de datos de previsión en el presupuesto de caja.
Esta sección muestra cómo se utilizan los datos de pronóstico en un presupuesto de efectivo. Además de la información del ejemplo anterior, suponga lo siguiente:
- Toda la producción se vende inmediatamente después de la producción.
- El precio de venta es de 2.000 dólares EE.UU. por tonelada.
- La venta se realiza con un plazo de crédito de cuatro semanas.
Los siguientes ingresos aparecerían en el presupuesto de efectivo para las semanas 12 a 16.

Tenga en cuenta que las ganancias de las semanas 12 y 13 se refieren a la producción real de las semanas 8 y 9 debido al retraso. Los datos de pronóstico de las semanas 10 a 12 se utilizan para calcular los ingresos de las semanas 14 a 16.
A continuación se muestra un estudio de caso que muestra cómo se puede utilizar la misma técnica para pronosticar datos de precios para un presupuesto de efectivo.
Estudio de caso: Previsión de precios estacionales
situación
Un supermercado compra knawberries, una popular fruta blanda, de tres
Fuentes. El proveedor utilizado depende de la época del año como se indica a continuación.
- Invernadero del Reino Unido: entre enero y abril, las Knawberries se compran a productores del Reino Unido que cultivan las plantas en invernaderos (esto significa que cosechan antes que las plantas cultivadas al aire libre).
- Reino Unido al aire libre: entre mayo y agosto, las Knawberries se compran a agricultores del Reino Unido que cultivan la fruta al aire libre.
- En el extranjero: entre septiembre y diciembre, las Knawberries se obtienen de productores extranjeros cuyo clima permite la producción durante el invierno británico.
A continuación se muestran los precios que el supermercado ha pagado a los proveedores durante los últimos tres años.

La necesidad mensual de fruta, que constituye la base para las necesidades de compra, ya se ha calculado para los meses de abril a octubre del cuarto año. Estos datos se presentan de la siguiente manera:
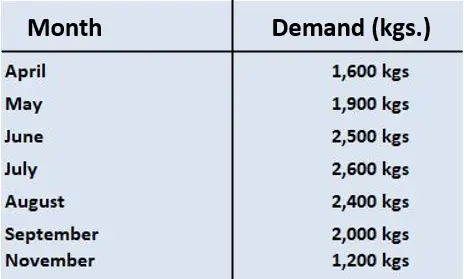
A todos los productores se les paga con un préstamo a dos meses.
Necesario:
- Utilizando un promedio móvil de tres puntos y teniendo en cuenta las fluctuaciones estacionales, pronostique los precios de compra que se pagarán en el cuarto año.
- Muestre un extracto de la sección Pagos del presupuesto de efectivo del año 4 de junio a noviembre relacionado con Knawberry.
Solución
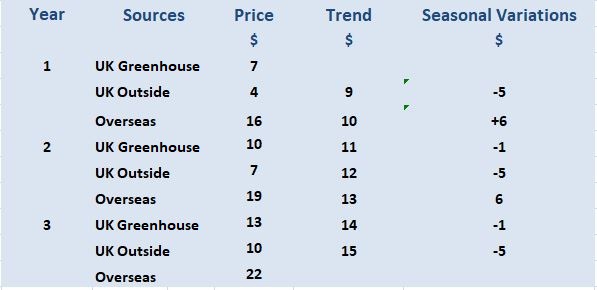
La tendencia de los precios aumenta 1 dólar cada temporada. Podemos utilizar esto junto con las fluctuaciones estacionales para predecir los precios en el cuarto año.

Ahora podemos utilizar los datos de la demanda junto con los precios previstos y el plazo del préstamo para crear el estado de pago del presupuesto de efectivo.

Cabe señalar que los montos pagados en junio se refieren a compras realizadas en abril. Esto se debe al plazo del préstamo. Por lo tanto, las cantidades de junio se basan en 1.600 kg a 16 dólares.
Asimismo, los pagos de julio-octubre se basan en precios externos y volúmenes de mayo-agosto. El pago de noviembre se aplica a los productos extranjeros comprados en septiembre a 25 dólares el kg.
Preguntas frecuentes sobre análisis de series temporales y fluctuaciones estacionales
Una serie de tiempo es una serie de puntos de datos recopilados en intervalos de tiempo fijos.
El análisis de series de tiempo puede proporcionar información sobre una variedad de problemas comerciales, incluidos el pronóstico de la demanda, la detección de tendencias y la estacionalidad. También puede ayudar a mejorar la toma de decisiones al suavizar las fluctuaciones en una serie temporal.
Una media móvil es una media aritmética que se calcula sumando el valor de la observación actual a la anterior y dividiendo la suma por dos. El proceso continúa hasta que se hayan utilizado todas las observaciones. Luego comienza de nuevo con la observación más reciente.
Las fluctuaciones estacionales son cambios que ocurren a intervalos fijos y se deben a factores predecibles como el clima. Pueden afectar a la demanda, la oferta y los movimientos de precios y deben tenerse en cuenta al pronosticar los precios.
Se puede utilizar una media móvil de tres puntos para suavizar las fluctuaciones en una serie temporal y proporcionar un pronóstico más preciso. Se calcula sumando la observación actual a las dos anteriores y dividiendo la suma por tres. Luego, este proceso se repite para cada nueva observación.
[automatic_youtube_gallery type=»search» search=»Análisis de series temporales y variaciones estacionales.
» limit=»1″]