¿Te gustaría aprender cómo calcular el valor presente de una anualidad? Si estás interesado en comprender cómo evaluar el valor actual de una serie de pagos fijos a lo largo del tiempo, estás en el lugar correcto. En este artículo, te explicaremos de manera clara y sencilla qué es el valor presente de una anualidad y cómo se calcula. No importa si eres estudiante, inversionista o simplemente alguien curioso por las finanzas, ¡esta información te será de gran utilidad!
Valor presente de una anualidad: definición
El valor presente de una anualidad se refiere al valor presente de una serie de promesas futuras de pagar o recibir una anualidad a una tasa de interés específica.
El valor presente de una serie de pagos o ingresos iguales que se realizarán o recibirán en fechas futuras específicas se denomina valor presente de una anualidad.
Valor presente de una anualidad: explicación
Al igual que con el valor futuro de una anualidad, los ingresos o pagos ocurren en el futuro. El valor presente es el valor actual, y el valor futuro se refiere al valor futuro acumulado.
El valor presente de una serie de pagos o recibos será menor que el total del mismo pago o recibos. Esto se debe a que el efectivo recibido en el futuro no es tan valioso como el efectivo recibido hoy.
Por otro lado, el valor futuro de una anualidad será mayor que la suma de los pagos o ingresos individuales porque se acumulan intereses sobre los pagos.
Es importante distinguir entre el valor futuro y el valor presente de una anualidad. Los horarios también son útiles aquí.
Las hipotecas y ciertos bonos de pago igual son ejemplos de problemas con el valor en efectivo de la anualidad.
Supongamos que un banco le presta hoy 60.000 dólares, que debe devolver en cuotas mensuales iguales a lo largo de 30 años.
En este caso, el banco quiere saber qué serie de pagos mensuales, descontando el tipo de interés acordado, corresponde al valor actual del importe del préstamo hoy.
Determinar el valor presente de una anualidad
Suponga que desea determinar el valor actual de recibir $1,00 al final de cada uno de los próximos 4 años. La tasa de interés o descuento apropiada es del 12%. Para resolver este problema, podemos crear una tabla que determine el valor actual de cada ingreso.
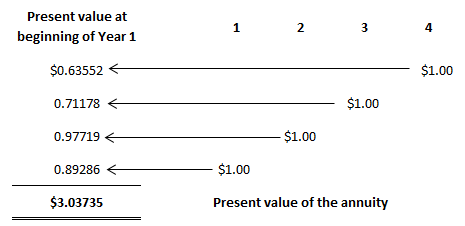
Por lo tanto, el valor presente de recibir los cuatro pagos de $1,00 es $3,03735 cuando se descuenta al 12%. Cada dólar individual se descontó utilizando factores en la tabla del valor presente de una cantidad única (ver más abajo).
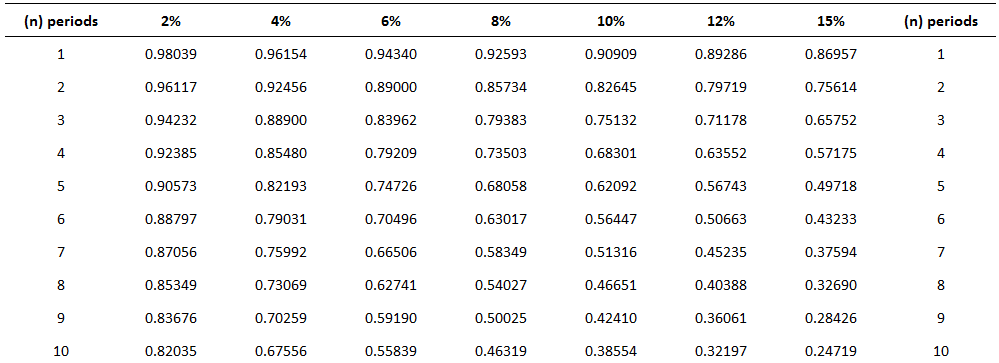
Por ejemplo, el valor presente del dólar recibido al final del cuarto año, descontado cuatro años, es $0,63552. Hay que calcular 4 años atrás porque el presente o hoy es el comienzo del primer año.
El dólar recibido al final del tercer año deberá descontarse por tres periodos; El dólar recibido al final del segundo año debe descontarse en dos periodos. Etcétera.
Al igual que para calcular el valor futuro de una pensión, podemos utilizar tablas preparadas. La siguiente tabla es un ejemplo de dicha tabla.
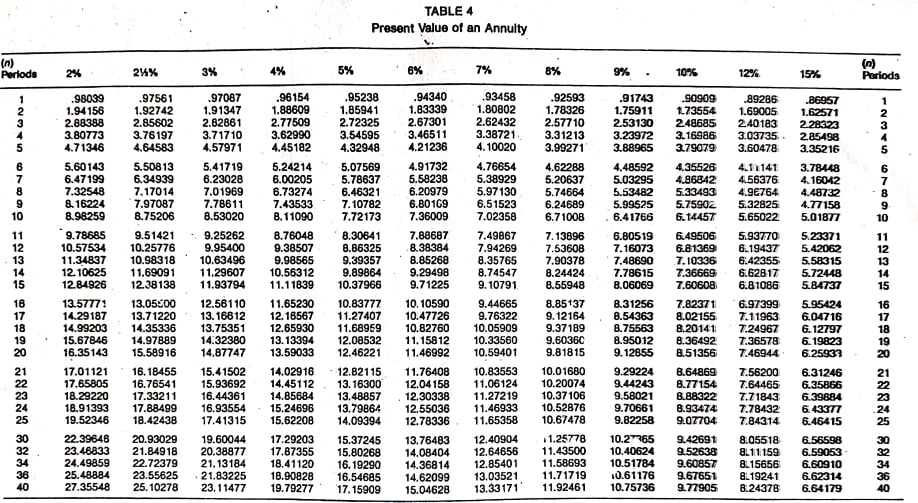
Esta tabla se crea sumando los valores presentes individuales de $1,00 a tasas de interés y períodos de tiempo específicos.
Por lo tanto, el factor para el valor presente de cuatro montos de $1,00 que se recibirán al final de cada uno de los próximos cuatro años descontados al 12% es 3,03735 (el valor que determinamos de forma independiente anteriormente).
Cuestiones relacionadas con el valor en efectivo de una anualidad
Los problemas que involucran el valor presente de una anualidad se resuelven utilizando la siguiente fórmula general:
Valor actual de una pensión = factor x monto de la pensión
Siempre que conozcamos dos de las tres variables, podemos resolver la tercera. Esto nos permite determinar el valor presente de la anualidad, la tasa de interés, el número de períodos o el monto de la anualidad.
Determinación del valor presente.
Para ilustrar cómo se calcula el valor presente de una anualidad, suponga que le ofrecen una inversión que pagará $2000 por año al final de cada uno de los próximos 10 años.
¿Cuánto pagarías por la inversión si quisieras obtener un retorno del 8%?
Esta es una cuestión de valor presente porque pagaría el valor actual de este flujo de efectivo con un descuento del 8%. Este monto es de $13,420.16 y se determina de la siguiente manera:
Valor actual de una pensión = factor x monto de la pensión
= 6,71008 x 2.000 dólares
= $13.420,16
Otra forma de interpretar este problema es decir: si quieres ganar el 8%, no hay diferencia si conservas $13.420,16 hoy o recibes $2.000 al año durante 10 años.
Determinación del pago de la pensión.
Una variante común de los problemas del valor presente es el cálculo del pago de la anualidad. En muchos casos, se trata de problemas crediticios o hipotecarios.
Digamos que compras una casa por $100,000 y haces un pago inicial del 20%. Tiene la intención de pedir prestado el resto del dinero al banco a una tasa de interés del 10%.
Para simplificar el problema, supongamos que realiza 30 pagos anuales al final de cada uno de los próximos 30 años. ¿A cuánto ascenderán sus pagos anuales?
En este caso, necesitará obtener un préstamo de $80 000 ($100 000 x 80%). Por lo tanto, el pago anual sería de $8,486.34 y se determinaría de la siguiente manera:
Valor actual de una pensión = factor x monto de la pensión
Monto de la pensión = valor presente de una pensión / factor
= $80.000 / 9,42691
= $8.486,34
Determinación del número de pagos.
Supongamos que Black Lighting Co. compró una nueva imprenta por $100 000. Los pagos trimestrales son de $4326,24 y la tasa es del 12% anual (o 3% trimestral).
¿Cuántos pagos se requieren para liquidar el préstamo?
En este caso, se requieren 40 pagos. Esto se determina de la siguiente manera:
Valor actual de una pensión = factor x monto de la pensión
Factor = valor actual de una pensión / monto de la pensión
= $100.000 / $4.326,24
= 23.11477
Si miramos hacia abajo en la columna del 3% en la Tabla 2, encontramos un factor de 23,11477 en el cuadragésimo período. Esto significa que se requieren 40 pagos trimestrales para liquidar el préstamo.
Problemas de combinación
Muchas aplicaciones contables relacionadas con el valor del dinero en el tiempo incluyen tanto cantidades individuales como anualidades.
Supongamos que está pensando en comprar un apartamento. Después de pensarlo mucho, llega a la conclusión de que obtiene un flujo de efectivo anual neto de $10,000 de los ingresos por alquiler menos el costo de alquilar el apartamento.
Para simplificar el análisis, suponemos que los flujos de efectivo se generan al final de cada año. Estos flujos de efectivo durarán 20 años. En este punto, usted estima que puede vender la casa por $250 000.
¿Cuánto deberías pagar por el edificio si quieres obtener una rentabilidad del 10%?
Este problema implica una anualidad (los flujos de efectivo netos anuales de 10 000 dólares) y una cantidad única (los 250 000 dólares que se recibirán una vez al final del vigésimo año).
Como persona racional, lo máximo que estaría dispuesto a pagar sería el valor actual de estos dos flujos de efectivo descontados al 10%. Este valor es $122,296, como se determina a continuación.
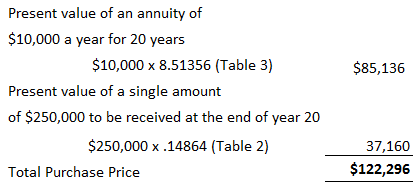
Preguntas frecuentes sobre el valor en efectivo de una anualidad
El valor presente de una anualidad es el valor o costo actual de un flujo fijo de pagos futuros. Esto se puede determinar descontando cada flujo de efectivo a una tasa de interés específica. Esto se puede calcular utilizando varias herramientas financieras, incluidas hojas de cálculo y calculadoras disponibles en Internet o en libros de hojas de cálculo.
El término «valor presente» se refiere a un flujo de efectivo único en un momento específico, mientras que el término «anualidad» se usa de manera más general para referirse a una serie de flujos de efectivo. El valor presente de una anualidad es un cálculo que se utiliza para determinar el valor o costo actual de un flujo fijo de pagos futuros. Por el contrario, el factor de anualidad calcula cuánto dinero se debe invertir a una determinada tasa de rendimiento durante un determinado período de tiempo para alcanzar una determinada cantidad en el futuro.
La tabla de valor presente de la anualidad contiene los factores utilizados para determinar un flujo de efectivo único en un momento específico. Esto se puede lograr descontando cada flujo de efectivo a una tasa específica utilizando varias herramientas financieras, incluidas hojas de cálculo y calculadoras.
Para determinar un flujo de efectivo individual o un factor de anualidad utilizando esta tabla, busque la cantidad de períodos en la fila superior y la tasa de interés (o tasa de descuento) en la parte inferior izquierda. Si introduce estos valores en una ecuación, obtendrá el valor presente de una anualidad.
Se puede determinar un flujo de efectivo o anualidad individual descontando cada flujo de efectivo a una tasa de interés específica utilizando varias herramientas financieras, incluidas hojas de cálculo y calculadoras. El término «valor presente» se refiere a un flujo de efectivo único en un momento específico, mientras que el término «anualidad» se usa de manera más general para referirse a una serie de flujos de efectivo.